| Lorentz Transformation | |
 |  |
A Lorentz transformation is a four-dimensional transformation
 | (1) |
satisfied by all four-vectors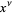 
, where 
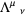is a so-called Lorentz tensor. Lorentz tensors are restricted by the conditions
, where is a so-called Lorentz tensor. Lorentz tensors are restricted by the conditions  | (2) |
with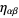 
the Minkowski metric (Weinberg 1972, p. 26; Misner et al. 1973, p. 68).
the Minkowski metric (Weinberg 1972, p. 26; Misner et al. 1973, p. 68). Here, the tensor indices run over 0, 1, 2, 3, with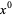 
being the time coordinate and 
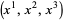are space coordinates, and Einstein summation is used to sum over repeated indices. There are a number of conventions, but a common one used by Weinberg (1972) is to take the speed of light 
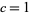to simplify computations allow 
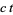to be written simply as 
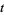for 
. The group of Lorentz transformations in Minkowski space 
is known as the Lorentz group.
being the time coordinate and are space coordinates, and Einstein summation is used to sum over repeated indices. There are a number of conventions, but a common one used by Weinberg (1972) is to take the speed of light to simplify computations allow to be written simply as for 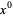. The group of Lorentz transformations in Minkowski space 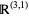is known as the Lorentz group. Note that while some authors (e.g., Weinberg 1972, p. 26) use the term "Lorentz transformation" to refer to the inhomogeneous transformation
 | (3) |
where 
is a constant tensor, the preferred term for transformations of this form is Poincaré transformation (Misner et al. 1973, p. 68). The corresponding group of Poincaré transformations is known as the Poincaré group.
is a constant tensor, the preferred term for transformations of this form is Poincaré transformation (Misner et al. 1973, p. 68). The corresponding group of Poincaré transformations is known as the Poincaré group. In the theory of special relativity, the Lorentz transformation replaces the Galilean transformation as the valid transformation law between reference frames moving with respect to one another at constant velocity. The Lorentz transformation serves this important role by virtue of the fact that it leaves the so-called proper time
 |  |  | (4) |
 |  |  | (5) |
invariant. (Here, the convention 
is used.) To see this, note that
is used.) To see this, note that  |  |  | (6) |
 |  |  | (7) |
 |  |  | (8) |
 |  |  | (9) |
(Weinberg 1972, p. 27).
The set of all Lorentz transformations is known as the inhomogeneous Lorentz group or the Poincaré group. Similarly, the set of Lorentz transformations with 
is known as the homogeneous Lorentz group. Restricting the transformations by the additional requirements
is known as the homogeneous Lorentz group. Restricting the transformations by the additional requirements  | (10) |
and
 | (11) |
where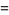 
denotes the tensor trace, give the proper inhomogeneous and proper homogeneous Lorentz groups.
denotes the tensor trace, give the proper inhomogeneous and proper homogeneous Lorentz groups. Any proper homogeneous Lorentz transformation can be expressed as a product of a so-called boost and a rotation.
REFERENCES:
Fraundorf, P. "Accel-1D: Frame-Dependent Relativity at UM-StL." http://www.umsl.edu/~fraundor/a1toc.html.
Griffiths, D. J. Introduction to Electrodynamics. Englewood Cliffs, NJ: Prentice-Hall, pp. 412-414, 1981.
Misner, C. W.; Thorne, K. S.; and Wheeler, J. A. Gravitation. San Francisco: W. H. Freeman, 1973.
Morse, P. M. and Feshbach, H. "The Lorentz Transformation, Four-Vectors, Spinors." §1.7 in Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 93-107, 1953.
Weinberg, S. "Lorentz Transformations." §2.1 in Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity. New York: Wiley, pp. 25-29, 1972.
